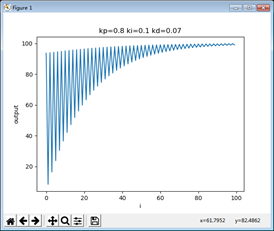
传统PID(位置式PID控制)调节：

这种算法的缺点是，由于全量输出，每次输出均与过去的状态有关，计算时要对

e(k) 进行累加，计算机运算工作量大。而且，因为计算机输出的 u(k) 对应的是执行机构的实际位置，如计算机出现故障， u(k) 的大幅度变化，会引起执行机构位置的大幅度变化，这种情况往往是生产实践中不允许的，在某些场合，还可能造成重大的生产事故，因而产生了增量式 PID 控制算法。

代码如下：

1 import matplotlib.pyplot as plt 2 class Pid: 3     def __init__(self,set_value = 100,now_value = 0,error_sum = 0,error_value = 0,error_last = 0,kp = 0,ki = 0,kd = 0): 4         self.set_value = set_value 5         self.now_value = now_value 6         self.error_sum = error_sum 7         self.error_value = error_value 8         self.error_last = error_last 9         self.kp = kp10         self.ki = ki11         self.kd = kd12 pid = Pid(100,100,0,0,0,0.7,0.1,0.1)13 data = []14 i = 10015 while i:16     pid.error_value = pid.set_value - pid.now_value17     pid.error_sum += pid.error_value18     pid.now_value = pid.kp * (pid.error_value + pid.ki * pid.error_sum + pid.kd * (pid.error_value - pid.error_last))19     print(pid.now_value)20     data.append(pid.now_value)21     pid.error_last = pid.error_value22     i = i - 123 #打印输出图表的部分24 plt.plot(data)25 plt.title("kp=" + (str)(pid.kp) + " ki=" + (str)(pid.ki) + " kd=" + (str)(pid.kd))26 plt.ylabel('output')27 plt.xlabel('i')28 plt.show()

波形如下（kp,ki,kd的参数需自行调节）：

 

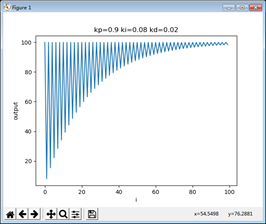
 增量式PID控制调节：

代码如下：

import matplotlib.pyplot as pltclass Pid:    def __init__(self,set_value = 100,now_value = 0,add_value = 0,last_value = 0,error_value = 0,error_last = 0,error_last_last = 0,kp = 0,ki = 0,kd = 0):        self.set_value = set_value        self.now_value = now_value        self.add_value = add_value        self.last_value = last_value        self.error_value = error_value        self.error_last = error_last        self.error_last_last = error_last_last        self.kp = kp        self.ki = ki        self.kd = kdpid = Pid(100,100,0,0,0,0,0,0.9,0.07,0.02)data = []i = 100while i:    pid.error_value = pid.set_value - pid.now_value    pid.add_value = pid.kp * (pid.error_value - pid.error_last) + pid.ki * pid.error_value + pid.kd * (pid.error_value - 2 * pid.error_last + pid.error_last_last)    pid.now_value += pid.add_value    print(pid.now_value)    data.append(pid.now_value)    pid.error_last = pid.error_value    pid.error_last_last = pid.error_last    i = i - 1plt.plot(data)plt.title("kp=" + (str)(pid.kp) + " ki=" + (str)(pid.ki) + " kd=" + (str)(pid.kd))plt.ylabel('output')plt.xlabel('i')plt.show()

波形如下（（kp,ki,kd的参数需自行调节））：